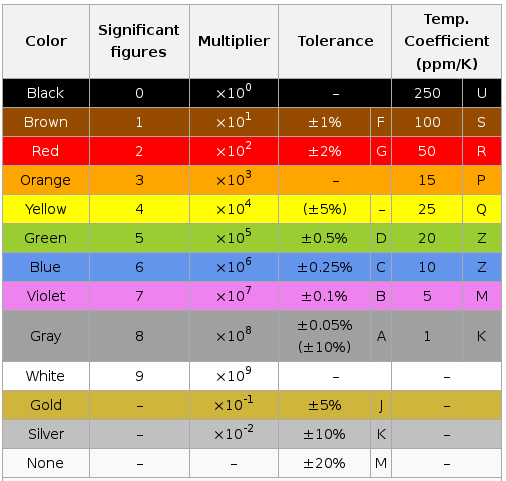
Display / Hide all schemas. | Power = watts | U = volts | R = \(\Omega\) | I = amperes | C = F (or µF (noted)) | f = Hz | T = tolerance
Resistors: Calculation with the lowest tolerance \(R-=R-\left(\frac{R \times T}{100}\right)\) | Calculation with the highest tolerance \(R+=R+\left(\frac{R \times T}{100}\right)\)
NB: a numeric value >= 0 is required in the input fields.
Resistors: Calculation with the lowest tolerance \(R-=R-\left(\frac{R \times T}{100}\right)\) | Calculation with the highest tolerance \(R+=R+\left(\frac{R \times T}{100}\right)\)
NB: a numeric value >= 0 is required in the input fields.
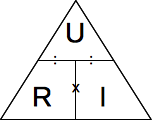
\(I=\frac{U}{R}\ \text{or}\ R=\frac{U}{I}\)
NaN or Infinity in I or R? Check if \(R\ \text{or}\ I>0\) - Top
NaN or Infinity in I or R? Check if \(R\ \text{or}\ I>0\) - Top

\(U\)
\(R\ \text{or}\ I\) -
\(I\ \text{or}\ R\)
\(U=\frac{P}{I}\ \text{or}\ I=\frac{P}{U}\)
NaN or Infinity in U or I? Check if \(I\ \text{or}\ U>0\) - Top
NaN or Infinity in U or I? Check if \(I\ \text{or}\ U>0\) - Top

\(P\)
\(I\ \text{or}\ U\) -
\(U\ \text{or}\ I\)
\(R=\frac{U}{I} \text{and}\ I=\frac{P}{U} \Rightarrow R=\frac{U}{P/U} \Rightarrow R=\frac{U^2}{P} \text{and}\ P=\frac{U^2}{R}\)
NaN or Infinity in R or P? Check if \(P\ \text{or}\ R>0\) - Top
NaN or Infinity in R or P? Check if \(P\ \text{or}\ R>0\) - Top

\(U\)
\(P\ \text{or}\ R\) -
\(R\ \text{or}\ P\)
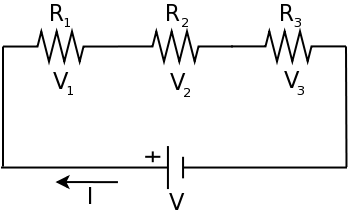
Resistors in serie (Value 0 = no resistor). 

\(eqR_s = \sum_{n=1}^{n=5}R_n = R_1 + R_2 + R_3 + R_4 + R_5\) - Top
\(R_1\)
\(R_2\)
\(R_3\)
\(R_4\)
\(R_5\) -
\(eqR_s\)
\(eqR-\)
\(eqR+\)
Resistors in parallel (Value 0 = no resistor). The division by 0 is handled.
\(\frac{1}{eqR_p} = \sum_{n=1}^{n=5}\frac{1}{R_n} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \frac{1}{R_4} + \frac{1}{R_5}\) - Top 

\(R_1\)
\(R_2\)
\(R_3\)
\(R_4\)
\(R_5\) -
\(\sum_{n=1}^{n=5}\frac{1}{R_n}\)
\(eqR_p\)
\(eqR-\)
\(eqR+\)
\(\Delta;U > 0\) and \(f > 0\) are required, the division by 0 is handled.
\(C_{\mu F}=\frac{I}{\Delta U \times f} \times 10^6\) - Top 

\(I\)
\(\Delta U\)
\(f\) -
\(C_{\mu F}\)
Capacitors in serie (Value 0 = no capacitor). The division by 0 is handled.
\(\frac{1}{eqC_s} = \sum_{n=1}^{n=5}\frac{1}{C_n} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + \frac{1}{C_4} + \frac{1}{C_5}\) - Top 

\(C_1\)
\(C_2\)
\(C_3\)
\(C_4\)
\(C_5\) -
\(\sum_{n=1}^{n=5}\frac{1}{C_n}\)
\(eqC_s\)
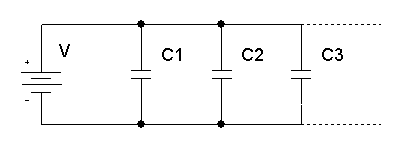
Capacitors in parallel (Value 0 = no capacitor). 

\(eqC_p = \sum_{n=1}^{n=5}C_n = C_1 + C_2 + C_3 + C_4 + C_5\) - Top
\(C_1\)
\(C_2\)
\(C_3\)
\(C_4\)
\(C_5\) -
\(eqC_p\)
Voltage divider. The division by 0 is handled.
\(U_2 = U\times \left(\frac{R_2}{R_2+R_1}\right)\) - Top 

\(U\)
\(R_1\)
\(R_2\) -
\(U_2\)
\(U_2=f(R1+, R2-)\)
\(U_2=f(R1-, R2+)\)
Note: With the formula, when we take the lowest tolerance for R1 AND R2, this will tend to annul the total effect of the two tolerances. Ditto for the highest tolerance. For an equal tolerance, the total effect is completely canceled. So, to get the most significant differences, we first compute with the highest tolerance for R1 and the lowest it for R2, then the opposite.
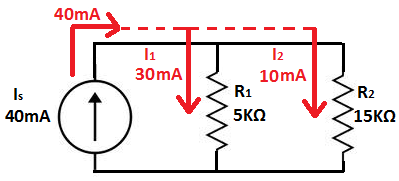
Current divider. The division by 0 is handled. 

\(I_1 = I\times \left(\frac{R_2}{R_2+R_1} \right)\) | \(I_2 = I\times \left(\frac{R_1}{R_2+R_1} \right)\) - Top
\(I\)
\(R_1\)
\(R_2\) -
\(I_1\)
\(I_1=f(R1+, R2-)\)
\(I_1=f(R1-, R2+)\)
\(I_2\)
\(I_2=f(R1+, R2-)\)
\(I_2=f(R1-, R2+)\)
Note: With the formula, when we take the lowest tolerance for R1 AND R2, this will tend to annul the total effect of the two tolerances. Ditto for the highest tolerance. For an equal tolerance, the total effect is completely canceled. So, to get the most significant differences, we first compute with the highest tolerance for R1 and the lowest it for R2, then the opposite.